Tlakové ztráty v perforovaných vzduchovodech
Článek přináší základní přehled o vnitřní aerodynamice v perforovaných vzduchovodech se zaměřením na tlakové ztráty a rovnoměrnou distribuci vzduchu z těchto vzduchovodů. Jsou v něm uvedeny faktory, které ovlivňují tyto ztráty, a tím i rovnoměrnost výtoku vzduchu. Vysvětluje předpoklady a problémy ohledně stanovení tlakových ztrát v těchto vzduchovodech. Tyto předpoklady a problémy jsou dál porovnány s výsledky některých dílčích experimentů, simulace CFD a dříve publikovaných výsledků.
Úvod
V současnosti se pro distribuci vzduchu začínají více používat kromě běžných distribučních prvků např. vyústek i perforované vzduchovody. Jedná se o vzduchovody s otvory, jejichž vzájemná vzdálenost je menší než několik průměrů vzduchovodu, tak, aby mezi nimi nedošlo k vyrovnání rychlostních profilů. Tyto vzduchovody („vyústky“) jsou zároveň potrubím i distribučním či sběrným prvkem. Vzduch je z (do) těchto vyústek přiváděn perforací materiálu, přirozenou prodyšností u textilií a případně kombinací obojího.
Článek se zaměřuje jen na dnes nejčastěji používané případy, tzn. perforované vzduchovody pro přívod vzduchu s konstantním průřezem a speciálně na vzduchovody z textilií a fólií. Ostatní typy vzduchovodů jsou většinou používány pro speciální průmyslové účely.
Také od perforovaných vzduchovodů obvykle požadujeme rovnoměrné provětrání prostorů, které zajistíme rovnoměrným přívodem vzduchu ze vzduchovodů. Tento rovnoměrný přívod je ovlivněn jednak geometrií perforace (otvoru ve vzduchovodu), jednak vnitřní aerodynamikou – tlakovými ztrátami (zisky) a rychlostními poměry uvnitř vzduchovodů.
Základní informace
Výtok vzduchu ze vzduchovodů
Výtok vzduchu otvorem (perforací) ze vzduchovodů je obecně ovlivněn geometrií otvoru, statickým tlakem a rychlostí proudění ve vzduchovodu. Pro výtokovou rychlost vs vazké nestlačitelné tekutiny z otvoru bez vlivu proudění uvnitř vzduchovodu platí známý vztah:
(1)
kde μ je výtokový součinitel otvoru, Δp rozdíl statických tlaků před a za otvorem (ps1 − pb, viz dále) a ρ hustota vzduchu.
Obr. 1 Výtok vzduchu z otvoru ve vzduchovodu
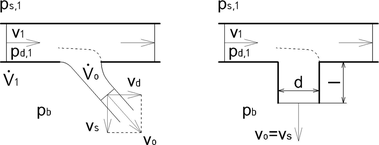
Při výtoku vzduchu ze vzduchovodu (obr. 1), u kterého je směr vektoru výtokové rychlosti odlišný od směru vektoru podélné rychlosti ve vzduchovodu v1 , dochází k odklonu vektoru výtokové rychlosti od kolmice k povrchu vzduchovodu. Pro velký ostrohranný otvor v tenké stěně se předpokládá při poměru průtoků 
do 0,4 až 0,5, že složky vektoru výtokové rychlosti budou tvořeny z rychlosti ve vzduchovodu vd (složka ve směru podél vzduchovodu) a teoretickou výtokovou rychlostí vs (složka kolmá ke vzduchovodu) viz obr. 1 vlevo. Při poměru průtoků nad 0,4 až 0,5 bude podle Talijeva podélná složka vd:
(2)
Předchozí neplatí v případě, že je otvor proveden jako dostatečně dlouhý nátrubek (např. u textilních vzduchovodů s mikroperforací, kde je průměr perforací porovnatelný s tloušťkou textilie), protože tento nátrubek usměrní vytékající proud, viz obr. 1 vpravo. Obvykle postačuje, aby byl nátrubek delší než průměr otvoru d – poměr l/d > 1.
Odklon vystupujících proudů od kolmice k povrchu vzduchovodu je obvykle nežádoucí jev, protože významně mění předpokládané obrazy proudění v prostoru.
Rovnoměrný přívod vzduchu
Rovnoměrný přívod vzduchu do prostoru znamená, že výtok vzduchu je po celé délce vzduchovodu konstantní. V praxi se připouští malé odchylky od této hodnoty, protože tyto významně neovlivní proudění v prostoru.
Průběh tlaků ve vzduchovodech
Z Bernoulliho rovnice při proudění v perforovaných vzduchovodech vyplývá, že s poklesem průtoku podél vzduchovodu (dynamického tlaku) narůstá statický tlak, který je dále snižován tlakovými ztrátami. Pokud by v perforovaném vzduchovodu proudila ideální nestlačitelná tekutina, statický tlak by monotónně stoupal až k jeho konci.
Tyto změny statického tlaku uvnitř vzduchovodu s konstantním průřezem ale ovlivňují i rovnoměrný přívod vzduchu, viz rovnice (1). Proto je třeba tyto změny tlaku kompenzovat:
- Změnou plochy perforace, které se mění po délce vzduchovodu
- Seškrcením přebytečného stat. tlaku clonkami ve vzduchovodu – vzniknou odchylky
- Zvýšením tlakové ztráty (rozdíl tlaků) otvoru (perforace), tak aby změny statického tlaku ve vzduchovodu byly vůči nim zanedbatelné – tzv. komora stálého statického tlaku
Další možností kompenzace by byla změna geometrie otvoru (nátrubky, klapky částečně clonící perforaci,…) za účelem úpravy výtokového součinitele, která ale není obvykle technologicky výhodná, pokud neslouží pro zvýšení dosahu vystupujícího proudu (tryska).
Účinnost přeměny dynamického tlaku
Pro popis tlakových poměrů uvnitř vzduchovodů se velmi často zavádí účinnost přeměny dynamického tlaku na tlak statický η [2, 3, 4]:
(3)
definovaný jako poměr rozdílu statického tlaku ps za (index 2) a před (index 1) odbočením a dynamického tlaku pd před a za odbočením. Pro případy s nerovnoměrnými rychlostními profily může nabývat hodnot i vyšších než 1, protože ze vzduchovodu je odváděna vrstva vzduchu s menší kinetickou energií, než je kinetická energie celého proudu, která je vždy vyšší než odpovídá průměrné rychlosti podle průřezu [1, 2].
Vnitřní aerodynamika
Rychlostní profily
Specifikem proudění v perforovaných vzduchovodech je skutečnost, že dochází k prakticky plynulé změně rychlostních profilů v podélném směru vzduchovodu, např. obr. 2 a 3.
Na tvar a postupnou změnu profilů má vliv i umístění a tvar otvorů (perforací). Např. pokud bude perforace jen na jedné podélné straně vzduchovodu, bude docházet k poklesu rychlosti u protější strany a tím ke snižování rovnoměrnosti profilu. Na konci vzduchovodu, kde je již nízký průtok vzduchu, může dojít u protější strany i ke zpětnému proudění. Vyšší podélná rychlost u stěny s perforací je důsledkem nátoku vzduchu do perforací. Navíc v rovině kolmé na rovinu perforací bude odlišný rychlostní profil – rychlostní profil bude prostorově nesymetrický. Pokud ale bude vzduchovod rovnoměrně perforován (prodyšný) po celém svém obvodu nebo alespoň po jeho části, bude rychlostní profil velmi vyrovnaný, resp. bude se blížit ideálnímu obdélníkovému profilu, viz obr. 3.
Z uvedeného je zřejmé, že dochází také k významnému radiálnímu proudění směrem k perforaci, které také probíhá v celé délce vzduchovodu. Hodnoty radiální rychlosti jsou poměrně malé, řádově okolo 0,1 m/s, viz např. obr. 4. V celém objemu vzduchovodu tedy dochází k prostorovému proudění.
Tlakové ztráty
Tlakové ztráty v těchto vzduchovodech vznikají třením, změnou výše popsaných rychlostních profilů a odbočováním proudů směrem do otvorů (odbočky). Další tlakové ztráty jsou klasické oblouky a případně odbočky – větvení vzduchovodů.
Vzhledem k rychlostním poměrům (profilům) v perforovaných vzduchovodech je velmi obtížné stanovit jednotlivé složky tlakových ztrát. Pro třecí tlakové ztráty jsou hodnoty součinitele tření běžně dostupné pouze potrubí s vyvinutým rychlostním profilem a bez radiálního proudění. Pro místní ztrátu např. odbočením proudu jsou uváděné hodnoty součinitel místní tlakové ztráty pouze pro případy jednotlivého odbočení, kde do součinitele ztráty je zahrnuta i ztráta změnou (vyrovnáním) rychlostního profilu v úseku navazujícím za odbočení. Pro případy, kdy za jedním odbočením následují další, výsledky schází. U perforovaných vzduchovodů se věc komplikuje ještě tím, že otvory mohou být ve stěně umisťovány nepravidelně jak po jeho délce, tak i po obvodu. Tím se ztěžuje už popis geometrie vzduchovodu. U hustě perforovaných (prodyšných) vzduchovodů navíc přestávají být patrné jednotlivé odbočky proudu a celek vypadá jako plošné odsávání mezní vrstvy.
Tlakové ztráty třením
Ve snaze zjednodušit výpočty a vyhnout se neznámým případům se v případech krátkých vzduchovodů (poměr skutečné délky a hydraulického průměru do hodnoty zhruba 30 až 50) tlaková ztráta třením často neuvažuje, protože vůči ostatním změnám tlaku je malá. Velká část autorů uvažuje součinitel třecí tlakové ztráty konstantní po celé délce, protože změna součinitele třecí ztráty vlivem změny rychlosti je obvykle malá [1]. Se změnou součinitele třecích ztrát je nutno uvažovat až u velmi dlouhých vzduchovodů. Plynulou změnou třecích ztrát podél vzduchovodu se zabýval Hemzal [2], který odvodil vztah pro změnu součinitele s použitím Blasiova vztahu. Jinou cestu zvolili Moueddeb, Barrington a Barthakur [3], kteří na základě energetické rovnice a větě o změně hybnosti navrhli postup, při kterém není potřeba počítat třecí tlakové ztráty předem.
Tlakové ztráty místní
Vzhledem ke složitému proudění bylo publikováno jen několik málo možností, jak odděleně stanovit alespoň část místních tlakových ztrát. Pro tlakovou ztrátu změnou rychlostních profilů platí teoreticky odvozený vztah pro výpočet součinitele místní tlakové ztráty ζ [1]:
(4)
který tento dává do souvislosti s Coriolisovým α a Boussinesqovým β součinitelem (popis rychlostního profilu) před a za narušením profilů.
Podle Hemzala [2] je nejvýznamnější místní ztrátou náhlé rozšíření proudu po odbočení v přímém směru určené Bordovou ztrátou s vlivem nerovnoměrného rychlostního profilu.
Výpočetní postupy Moueddeba, Barringtona a Barthakura [3] (zmíněný výše) a dle Haertera [4] stanovují místní ztráty (účinnosti přeměny dynamického tlaku) z rychlostí před a za odbočením a výstupní rychlosti s uvažováním nerovnoměrných rychlostních profilů.
CFD simulace a publikované výsledky
Výše popsané jevy v perforovaných vzduchovodech jsou dobře vidět na výsledcích z CFD simulace kruhového vzduchovodu s mikroperforací o průměru 100 mm a délce 2000 mm (z pohledu výpočtu krátký vzduchovod) [1]. Přívod vzduchu do perforovaného vzduchovodu je kruhovým nepropustným potrubím o stejném průměru. Tento vzduchovod je umístěn ve velkém prostoru bez dalších stěn. Stěna vzduchovodu byla schematizována jako porézní vrstva („porous jump“) s tlakovou ztrátou, která odpovídá perforované tkanině s otvory o průměru zhruba 0,4 mm a hustotou perforace 150 000 otvorů/m2. Tato tlaková ztráta perforované tkaniny byla stanovena experimentálně, blíže viz [1].
![Obr. 2 Rychlostní pole v rovnoměrně perforovaném vzduchovodu a v jeho okolí, rychlosti v m/s, řez, osově symetrické [1]](/docu/clanky/0116/011601o8.png)
Obr. 2 Rychlostní pole v rovnoměrně perforovaném vzduchovodu a v jeho okolí, rychlosti v m/s, řez, osově symetrické [1]
Na obr. 2 jsou výsledné rychlostní pole ve vzduchovodu a v jeho okolí. Viditelné je především odklánění vzduchu vystupujícího z textilie a pokles rychlosti směrem od vstupu (vlevo) k zaslepenému konci vzduchovodu (vpravo). Úhel mezi vektorem rychlosti a povrchem vyústky je asi 8°. Za zaslepeným koncem vzduchovodu je patrný i malý úplav (velmi malá rychlost proudění).
Nevýhodou tohoto způsobu zadání stěny vzduchovodu („porous jump“) je to, že nedokáže simulovat změnu směru vzduchu proudícího přes tuto vrstvu, mikroperforace tkaniny se totiž chová jako krátký nátrubek. Model také nedokáže počítat tlakové ztráty třením, protože okrajová podmínka „porous jump“ se chová jako pomyslná tlaková ztráta vložená do proudu a ne jako pevná stěna. Vzhledem k malé délce vzduchovodu budou ale třecí ztráty poměrně malé. Model s reálně zadanými otvory ve stěně je totiž prakticky velmi těžko proveditelný a i výpočet by byl velmi složitý a zdlouhavý.
Axiální rychlostní profily ve vzduchovodu (v jeho osově symetrické polovině) jsou na obr. 3. Jasně jsou patrné změny rychlostních profilů, které se po určité deformaci po vstupu do perforovaného vzduchovodu začínají vyrovnávat. Ve vzdálenosti větší než 0,7 m od vstupu jsou rychlostní profily už velmi vyrovnané.
![Obr. 3 Axiální rychlostní profily v rovnoměrně perforovaném vzduchovodu [1]](/docu/clanky/0116/011601o10.png)
Obr. 3 Axiální rychlostní profily v rovnoměrně perforovaném vzduchovodu [1]
![Obr. 4 Radiální rychlostní profily v rovnoměrně perforovaném vzduchovodu [1]](/docu/clanky/0116/011601o12.png)
Obr. 4 Radiální rychlostní profily v rovnoměrně perforovaném vzduchovodu [1]
Na obr. 4 jsou průběhy radiálních rychlostí (rychlosti kolmé k ose) ve vzduchovodu. Je patrný vývin radiálních rychlostí, kdy rychlost stoupá směrem od vstupu do vyústky a směrem ke stěně. Na vstupu do vyústky (přívod z neprostupného potrubí) jsou radiální rychlosti nulové, protože vzduch nemůže přes pevnou stěnu vytékat. Nejvyšší radiální rychlosti jsou dosahovány v blízkosti stěny, kde se shodují s výtokovou rychlostí ze vzduchovodu.
Obr. 5 Poměrné statické tlaky v perforovaných vzduchovodech
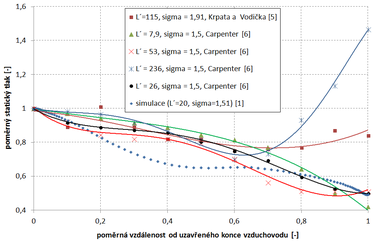
Na obr. 5 je průběh poměrného statického tlaku (vztažený ke statickému tlaku na konci vzduchovodu) v závislosti na poměrné vzdálenosti (vztaženo na délku vzduchovodu). Je zde uveden jak výsledek simulace, tak i experimentálně zjištěné hodnoty od několika autorů.
Průběh poměrných tlaků je uveden také v závislosti na poměrné délce L´ – poměru délky a hydraulického průměru. Všechny vzduchovody mají podobnou hodnotu poměrné průtočné plochy perforace σ – poměru plochy perforace a průřezu vzduchovodu. Je patrné, že s rostoucí délkou vzduchovodů se mění průběh tlaků. U krátkých vzduchovodů tlak monotónně stoupá, u dlouhých do vzdálenosti zhruba 0,6 klesá a následně stoupá vlivem velkých třecích ztrát po vstupu do vzduchovodu.
Z porovnání výsledků simulace a vzduchovodu s L´ = 26 vyplývá shoda jen na začátku a konci vzduchovodu. Způsobeno to bude zjednodušujícím zadáním perforované stěny v simulaci [1] a mírně odlišnou geometrií při měření – měřený vzduchovod [6] byl perforován velkými otvory na protilehlých stranách a byl delší.
Závěr
Příspěvek přináší základní přehled o problematice vnitřní aerodynamiky v perforovaných vzduchovodech, která má vliv i na proudění v prostoru – viz obr. 2, kde šikmo vystupující proud naruší předpokládané obrazy proudění v prostoru.
Dál seznamuje o komplikovanosti odděleného výpočtu jednotlivých tlakových ztráty vlivem významně se měnících rychlostních axiálních a radiálních profilů. Tlakové ztráty mají významný vliv na průběhy statických tlaků zvlášť u dlouhých vzduchovodů, viz obr. 5, kde díky nim dochází v blízkosti vstupu k poklesu statického tlaku a následně k jeho nárůstu. Znalost statických tlaků a jejich průběhů ve vzduchovodech je totiž důležitý parametr, který potřebujeme pro návrh velikosti otvorů (perforací).
I přes určité odchylky počítačového modelu v porovnání s naměřeným průběhem statického tlaku, dává simulace zajímavé a použitelné výsledky. Jedná se hlavně o velikost a směr proudění uvnitř vzduchovodu, u kterého by v reálném experimentu byla velmi těžko měřitelná radiální složka rychlostí. Z výsledků je patrné, že lze použít okrajovou podmínku „porous jump“ pro zadání (schematizaci) jemně perforované stěny jen v případě, že potřebujeme vyšetřit pouze rychlostní a tlakové pole uvnitř krátkého vzduchovodu.
Literatura
- [1] POSPÍŠIL, M. Vzduchovody pro rovnoměrný rozvod vzduchu. Studie dizertační práce, ČVUT v Praze, Fakulta strojní, 2012
- [2] HEMZAL, K. Příspěvek k návrhu vzduchovodů stálého průřezu pro rovnoměrný přívod vzduchu do klimatizovaných a větraných místností. ACTA POLYTECHNIKA, číslo II, 1977, str. 31 až 46, ČVUT v Praze
- [3] MOUEDDEB, K. El., BARINGTON, S., BARTHAKUR, S., BARTHAKUR, N. Perforated ventilation duct: Part . A model for air flow distribution, Journal of Agricultural Engineering Research, číslo 68, 1997, str. 21 až 27
- [4] HAERTER, A., Theoretische und experimentalle Untersuchungen über die Lüftungsanlagen von Straßentunneln. dizertační práce, ETH Bern, 1961
- [5] VODIČKA, M., KRPATA, L. Vzduchovody s neproměnným průřezem pro rovnoměrný přívod vzduchu. Práce studentského kroužku, ČVUT v Praze, Fakulta strojní, 1985
- [6] CARPENTER, G. A. The design of permeable ducts and their application to the ventilation of livestock buildings. Journal of Agricultural Engineering Research, číslo 3, ročník 17, 1972, str. 219 až 230
- [7] Firma Příhoda s. r. o. Webová stránka firmy, aktualizováno 16. 3. 2014. Dostupné z: http://www.prihoda.com/cs/
Článek vznikl s podporou grantů SGS 161-802540, 161-1326 a pomoci fi. Příhoda s. r. o.
The article presents an overview of the internal aerodynamics in perforated ducts with a focus on pressure loss and uniform distribution of the air in the ductwork. There are the factors that influence these losses and thus the uniformity of the outlet air. It explains assumptions and problems in determining of pressure losses in these ducts. These assumptions and problems are compared with the results of some individual experiments, CFD simulations and previously published results.
