Stanovení střední radiační teploty (I)
Operativní teplota je hodnotícím kritériem pro tepelnou pohodu v prostoru. Kromě teploty vzduchu respektuje i střední radiační teplotu a proudění vzduchu. V první části příspěvku autor vypočítává možnosti stanovení střední radiační teploty.
1. ÚVOD
Hodnotícím kriteriem pro tepelnou pohodu v prostoru podle Nařízení vlády č. 523/2002 Sb. [4] je operativní teplota to, která respektuje kromě teploty vzduchu ta i střední radiační teplotu tr (dříve účinná teplota okolních ploch, v zahraniční literatuře označovaná jako MRT - mean radiant temperature) a rychlost proudění vzduchu wa.
Operativní teplota je jednotná teplota uzavřeného černého prostoru, ve kterém by tělo sdílelo radiací a konvekcí stejně tepla, jako ve skutečném nehomogenním prostředí a vypočítá se podle vzorce
| (1) |
| A | hodnota závislá na relativní rychlosti proudění vzduchu [ - ] |
| ta | teplota vzduchu [ °C ] |
| tr | střední radiační teplota [°C ] |
| wa [m/s] | < 0,2 | 0,3 | 0,4 | 0,6 | 0,8 | 1 |
|---|---|---|---|---|---|---|
| A [ - ] | 0,5 | 0,53 | 0,6 | 0,65 | 0,7 | 0,75 |
Tab. 1 - Závislost součinitele A na rychlosti prouděni vzduchu v prostoru
Při rychlostech proudění vzduchu pod 0,2 m/s lze nahradit operativní teplotu výslednou teplotou tg, měřenou kulovým teploměrem.
| (2) |
Příslušný hygienický předpis uvádí, že střední radiační teplotu tr lze stanovit z výsledné teploty kulového teploměru tg. To je sice pravda, nicméně je to možné pouze v případě hotového díla, neboť teplotu kulového teploměru nezjistíme jinak než měřením. Otázkou tedy je, jakým způsobem střední radiační teplotu tr zjistí projektant, který zcela jistě k dispozici hotové dílo nemá, ale který se podle hygienického předpisu musí řídit.
Pro běžně projektované systémy větrání a klimatizace, kdy výrazně převažuje konvekční přenos tepla, se předpokládá, že teplota okolních stěn nebude výrazně odlišná od teploty vzduchu v místnosti a bude platit ta = tr = to. Projektanti navíc většinou nemají k dispozici výpočtovou metodu, s níž by bylo možné povrchovou teplotu stěn (střední radiační teplotu a z ní operativní teplotu) stanovit.
V případě použití sálavých chladicích / vytápěcích systému, však teplota vzduchu nebude shodná s teplotou okolních stěn. Naopak může se i výrazně lišit.
2. STŘEDNÍ RADIAČNÍ TEPLOTA
Množství tepla, sdíleného sáláním mezi povrchem těla a jednotlivými obklopujícími plochami v prostoru, lze stanovit výpočtem poměrně obtížně a zdlouhavě. K usnadnění výpočtu a k posouzení sálavého účinku všech okolních ploch jedinou veličinou, byla zavedena tzv. střední radiační teplota tr.
Střední radiační teplota tr je definována jako společná teplota všech okolních ploch, při které by bylo celkové množství tepla sdílené sáláním mezi povrchem těla a okolními plochami stejné jako ve skutečnosti. Pro obecný případ platí
| (3) |
| Tn | absolutní teploty povrchů okolních ploch Sn [ K ] |
| Frn | poměry osálání jednotlivých okolních ploch Sn plochou Sr (např. povrch lidského těla) |
pokud se vzájemně teploty t1, t2 ... tn příliš neliší, lze vztah (3) zjednodušit na tvar
| (4) |
| tn | teploty povrchů okolních ploch Sn [ °C ] |
někdy lze k výpočtu použít i přibližné rovnice, která v podstatě vyjadřuje střední teplotu okolních ploch
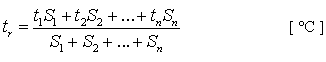 |
(5) |
Hodnota střední radiační teploty vypočítaná dle rovnice (4) v uvedené lineární formě je vždy poněkud nižší než hodnota dle rovnice (3), jak je vidět z příkladu uvedeném v kapitole 4. Ve většině případů je však rozdíl mezi oběma výsledky velmi malý. Pokud jsou rozdíly mezi teplotami povrchů velké, chyba může narůstat.
Podle ČSN EN ISO 7726 [6] se pro hodnocení tepelného prostředí v homogenním prostředí stanovuje střední radiační teplota tr ve výškách 0,6 m nad podlahou pro sedící a 1,1 m nad podlahou pro stojící osobu.
3. MOŽNOSTI STANOVENÍ STŘEDNÍ RADIAČNÍ TEPLOTY
V zásadě existují tři základní možnosti jak určit střední radiační teplotu tr
- manuálním výpočtem
- použitím simulačního programu
- měřením parametrů tepelného stavu prostředí
3.1. STANOVENÍ STŘEDNÍ RADIAČNÍ TEPLOTY VÝPOČTEM
Princip výpočtu střední radiační teploty spočívá ve stanovení poměrů osálání v libovolně definovaném bodě na základě geometrických poměrů vzájemné polohy mezi sálající a osálanou plochou (osobou).
3.1.1. POMĚR OSÁLÁNÍ
Poměr osálání Fn značí poměrný díl z celkově vysálaného tepla plochou Sr, který přijímá plocha Sn. Poměr osálání vyjadřuje geometrické poměry při sdílení tepla sáláním mezi dvěma plochami. Obecně poměr osálání závisí na vzájemné poloze sálající plochy a plochy osálané, dále pak na velikosti a vzdálenosti těchto ploch.
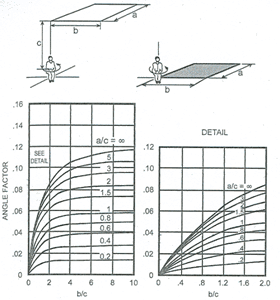
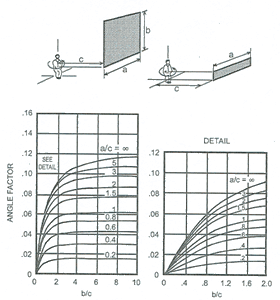
Problémem stanovení poměrů osálání se zabýval Fanger [3], který provedl experimentální rozbor pro základní případy vzájemné polohy mezi sedícím či stojícím člověkem a vodorovnou či svislou plochou. Zjištěné hodnoty poměrů osálání vynesl jako grafické závislosti (Obr. 1) na geometrických parametrech výpočtu (Fangerovy grafy jsou součástí ČSN EN ISO 7726 [6]). Z takto vytvořených závislostí je možné odečítat hodnoty poměrů osálání pro zadané geometrické uspořádání. I když jsou publikované výsledky stále platné, řešení pomocí odečítání hodnot poměrů osálání z grafů je časově náročné a v dnešním světě počítačů již skoro nemyslitelné.
 a) |
 b) |
Obr. 1 - Střední hodnoty poměrů osálání podle Fangera
a) mezi sedící osobou a vodorovným obdélníkem, b) mezi sedící osobou a svislým obdélníkem
3.1.2. ZJEDNODUŠENÝ VÝPOČET POMĚRŮ OSÁLÁNÍ
Ve skutečnosti by tedy střední radiační teplota tr měla být vztažena k povrchu lidského těla (St = 1,8 m2), avšak pro zjednodušení se vztahuje k povrchu elementární koule resp. k bodu umístěnému v těžišti člověka. Pro sálající bod definovaný podle Obr. 2a) platí [2]
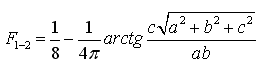 |
(6) |
3.1.3. ADIČNÍ PRAVIDLO
Stanovení poměrů osálání F tedy není zcela jednoduchou záležitostí, zejména pokud se jedná o geometricky složité případy. Ke zjednodušení složitějších případů slouží adiční pravidlo, které plyne ze zákona o zachování energie. Podle něj se poměr osálání obecné plochy S1 složené z dílčích ploch plochou S2, rovná součtu poměrů osálání jednotlivých dílčích ploch. Pro případ podle Obr. 2b), kdy je bod 1 osálán plochou 2 bude platit
| (7) |
Pro případ podle Obr. 2c) kdy je bod 1 osálán plochou 2, která leží mimo spojnici s bodem 1 bude platit
| (8) |
kde poměry osálání FI, FII,FIII,FIV vypočítáme podle vztahu (6) s odpovídajícími parametry a, b a h pro jednotlivé plochy
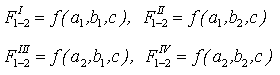 |
V případě, že je sálající plocha S1 (osoba) zcela obklopena plochou S2 (místnost), bude pro součet všech poměrů osálání mezi elementární koulí (nahrazující člověka) a jednotlivými stěnami platit
| (9) |
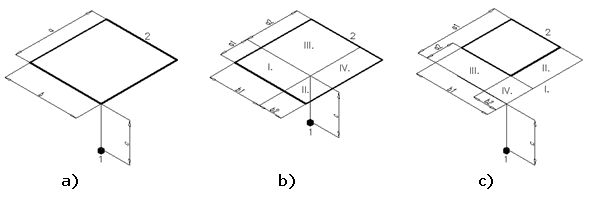
Obr. 2 - Parametry pro výpočet poměru osálání
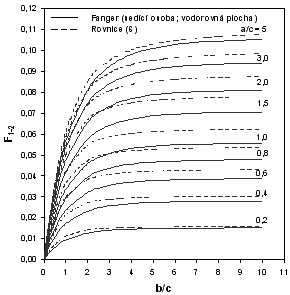
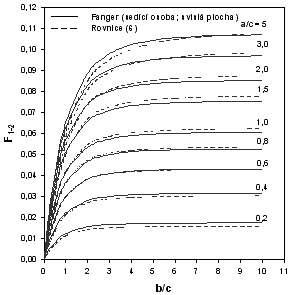
Na Obr. 3 jsou zobrazeny hodnoty poměrů osálání vypočtených podle rovnice (6) (čárkovaně) společně s Fangerovými závislostmi (plně). Na první pohled je zřejmé, že pro případ výpočtu mezi sedící osobou a vodorovnou plochou (Obr. 3a) jsou mezi oběma výsledky určité rozdíly. Naproti tomu pro případ mezi sedící osobou a svislou stěnou (Obr. 3b) jsou rozdíly mezi výsledky minimální a výsledky výpočetního postupu (6) velmi dobře korespondují s hodnotami zjištěnými z Fangerových grafických závislostí.
 a) |
 b) |
Obr. 3 - Porovnání poměrů osálání podle rovnice (6) s Fangerovými grafickými závislostmi
a) mezi sedící osobou a vodorovným obdélníkem (strop, podlaha) SED -V, b) mezi sedící osobou a svislým obdélníkem (stěny) SED -S
SEZNAM LITERATURY:
[1] ASHRAE Handbook 2001 Fundamentals, 2001, ASHRAE, Atlanta. ISBN - 1-883413-87-7
[2] CIHELKA, J., a kol. Vytápění a větrání. 1969, Praha: SNTL. ISBN 04-216-75
[3] FANGER, P.O. Thermal comfort - Analysis and applications in enviromental engineering. 1972, Kingsport Press, Inc. ISBN 07-019915-9
[4] Nařízení vlády č. 523/2002 Sb., kterým se mění nařízení vlády č. 178/2001 Sb., kterým se stanoví podmínky ochrany zdraví zaměstnanců při práci
[5] Vyhláška č. 137/2004 o hygienických požadavcích na stravovací služby a o zásadách osobní a provozní hygieny při činnostech epidemiologicky závažných
[6] ČSN EN ISO 7726: 1993 Tepelné prostředí - Přístroje a metody měření fyzikálních veličin, ČSNI 1993
[7] SARS, G., PERNOT, C., De WIT, M. ESPmrt, a new module for the ESP-r system, University of Technology Eindhoven. Institute of Applied Physics TNO-TH, April 1988
[8] ZMRHAL V. Tepelný komfort a energetická bilance systému s chladicím stropem. 2005, Disertační práce, ČVUT.
Příspěvek byl napsán s podporou výzkumného záměru MSM 6840770011.