Teorie vlhkého vzduchu a úprava vlhkosti vzduchu při větrání (I)
Úvod a vyjádření vlhkosti vzduchu
Teorie vlhkého vzduchu a způsoby vyjádření vlhkosti vzduchu jsou doplněny komentáři. Základní informace pro návrh úpravy vlhkosti vzduchu při větrání.
1. Úvod
Vlhký vzduch je směs suchého vzduchu a určitého množství vody ve formě syté, či přehřáté vodní páry, mlhy, jinovatky.
1.1 Daltonův zákon
Pro výpočty tepelných procesů se používá Daltonův zákon: celkový tlak směsi plynů p je dán součtem dílčích (parciálních) tlaků jednotlivých složek pi:
![]()
Vzhledem k této skutečnosti lze rozepsat barometrický tlak do jednotlivých složek:
![]()
Poznámka:
Problematiku indexování provázejí spory a v různých literaturách se liší. V tomto dokumentu se vychází z platných norem ČSN EN 12792, ČSN EN ISO 7730 a ČSN EN ISO 7726. Značení vodní páry bude provedeno indexem "V" (angl. "vapour") a suchého vzduchu indexem "A". Pro vodní páru se také často používá index "D" (něm. "dampf") a pro suchý vzduch index "L" (něm. "luft"). V české literatuře se pro suchý vzduch používá index "s.v."
1.2 Stavová rovnice
Pro 1 kg vlhkého vzduchu má stavová rovnice tvar:
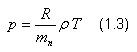
| p | [Pa] | celkový tlak vzduchu |
| R | [J/kmol.K] | univerzální plynová konstanta (R = 8 314,3 J/kmol.K) |
| ρ | [kg/m3] | hustota (měrná hmotnost) vlhkého vzduchu |
| T | [K] | termodynamická teplota |
| mn | [kg/kmol] | střední molekulová hmotnost vlhkého vzduchu |
Poznámka:
Odchylka parametrů vlhkého vzduchu v rozmezí teplot (200 až 500) K a tlaků (0,1 až 1,0) MPa je od stavové rovnice pro ideální plyn menší než 3 %. Pro vodní páru do tlaku 1 kPa je odchylka ještě menší.
Molekulová hmotnost suchého vzduchu mA = 28,96 kg/kmol
Molekulová hmotnost vodní páry mV = 18,02 kg/kmol
Plynové konstanty mají hodnotu:
rA = 287,11 J/kg.K
rV = 461,50 J/kg.K
Poznámka:
1/ρ má jednotky [1/(kg/m3) = m3/kg], což je měrný objem (v = 1/ρ), bývá stavová rovnice pro ideální plyn zapisována ve tvaru p . v = r . T
Vztah 1.2. určuje výsledný tlak (barometrický) směsi suchého vzduchu a vodní páry. Například pro vlhký vzduch o teplotě t = 20 °C, relativní vlhkosti φ = 50 % a tlaku p = 98 kPa platí, že parciální tlak vodní páry je pV = 1,17 kPa. Tlak suchého vzduchu tedy bude pA = 96,83 kPa.
2. Vyjádření vlhkosti vzduchu
Obsah vlhkosti ve vzduchu může být různý. Vlhký vzduch se dělí na:
- nenasycený (parciální tlak vodních par ve vzduchu je menší tlak sytých par při téže teplotě pV < pV"
- nasycený pV = pV"
- přesycený (nasycený vzduch, který obsahuje ještě další vodu v kapalném nebo tuhém skupenství)
Poznámka:
Pára sytá - Pára, která je v termodynamické rovnováze se svou kapalnou fází. Její tlak je určen pouze teplotou. Zmenšuje-li se objem při stálé teplotě a tlaku, pára kondenzuje. Při zvětšování objemu se kapalná fáze vypařuje, až zbude jen sytá pára. Při dalším zvětšování objemu není již kapalinou nasycena a stává se z ní pára přehřátá. Zdroj: www.wikipedia.cz.
Veličin určujících vlhkost vzduchu je několik:
2.1 Absolutní vlhkost vzduchu a, ρV
Hmotnost vodní páry v objemu 1 m3. Jednotky jsou kg/m3 a dá se proto také hovořit o hustotě vodní páry ρV.
2.2 Relativní vlhkost φ
Udává míru nasycení vzduchu. φ = 100 % znamená nasycený vzduch; pV = pV".
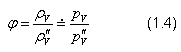
Poznámka:
Pouze přibližná rovnost je dána skutečností, že vlhký vzduch není ideální plyn.
2.3 Parciální tlak par pV
Tlak, odpovídající příslušné absolutní vlhkosti (viz stavová rovnice). Parciální tlak par není závislý na teplotě (při konstantním tlaku).
Parciální tlak syté páry p"V je závislý pouze na teplotě a jeho hodnoty jsou uvedeny v příloze 1. Pro určení p"V lze také použít vztahy z literatury [3] pro teploty -20 až 0 °C s chybou menší než 1‰:
![]()
a pro teploty 0 až 80 °C s chybou menší než 1‰:
![]()
V literatuře [4] je uvedeno pro teploty -100 až 0 °C:
![]()
a pro teploty 0 až 200 °C platí:
![]()
| C1 | = -5,674 535 9.103 |
| C2 | = -5,152 305 8.10-1 |
| C3 | = -9,677 843 0.10-3 |
| C4 | = 6,221 570 1.10-7 |
| C5 | = 2,074 782 5.10-9 |
| C6 | = -9,484 024 0.10-13 |
| C7 | = 4,163 501 9 |
| C8 | = -5,800 220 6.103 |
| C9 | = -5,516 256 0 |
| C10 | = -4,864 023 9.10-2 |
| C11 | = 4,176 476 8.10-5 |
| C12 | = -1,445 209 3.10-8 |
| C13 | = 6,545 967 3 |
2.4 Měrná vlhkost vzduchu x
Udává hmotnost vodní páry v kg, připadající na 1 kg suchého vzduchu [kg/kgA]. Vzhledem k nízkým řádům se spíše používají jednotky [g/kgA]. Spolu s relativní vlhkostí je toto určení vlhkosti vzduchu ve vzduchotechnice nejběžnější. Měrná vlhkost je určena poměrem hmotnosti vodní páry obsažené ve vzduchu a hmotnosti suchého vzduchu:
![]()
Dosazením stavových rovnic pro suchý vzduch a vodní páru obdržíme vzájemný vztah mezi měrnou a relativní vlhkostí:
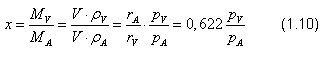
dalším dosazováním rovnic 1.2 a 1.4 dostaneme konečnou podobu:
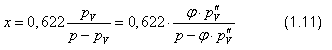
Vztah 1.11 je důležitý, neboť nám umožňuje stanovit měrnou vlhkost z měřitelných veličin (φ, p) a parciálního tlaku syté páry.
Po dalších úpravách lze získat další závislosti:
![]()
a dále z 1.4 a 1.8:
![]()
Poznámka:
Absolutní vlhkost vzduchu, relativní vlhkost a parciální tlak par jsou veličiny určující stav páry nezávisle na vzduchu. Měrná vlhkost je poměr hmotnosti vodní páry a suchého vzduchu. Dalšími možnostmi určení vlhkosti vzduchu jsou teplota rosného bodu a teplota mokrého teploměru. Tyto veličiny se dají získat měřením.
2.5 Teplota rosného bodu tDP
Teplota, při které je vzduch nasycen. Při dalším ochlazování začíná vodní pára kondenzovat. V h-x diagramu se teplota rosného bodu pro daný stav vzduchu odečte na průsečíku křivky nasycení a čáry měrné vlhkosti, odpovídající danému stavu vzduchu. Grafické znázornění v h-x diagramu je na obrázku 2.
Poznámka:
Pro teplotu rosného bodu tDP (angl. "Dew Point") se také často používá index "r"
2.6 Teplota mokrého teploměru tm (tWB)
Je to taková teplota vody, při níž je teplo potřebné k vypařování vody do vzduchu odebíráno přestupem tepla konvekcí z okolního vzduchu (při izobarickém ději). Je také označována jako mezní teplota adiabatického chlazení. Grafické znázornění v h-x diagramu je na obrázku 2. Teplota mokrého teploměru je také označována tWB (wet bulb).
2.7 Měření vlhkosti vzduchu
Způsoby měření vlhkosti jsou:
- měřením teploty rosného bodu (ochlazované zrcátko s optickým snímačem)
- měřením relativní vlhkosti na základě změny vlastností látek (ovčí střívko, vlas, kapacitní čidla, elektrická vodivost)
- zachycením vlhkosti z daného objemu vzduchu
- psychrometrem (teplota suchého tA a mokrého teploměru tWB)
Psychrometrická rovnice:
![]()
Kde A je psychrometrická konstanta (662.10-6 K-1)
Použitá literatura
[1] Chyský, J.; Vlhký vzduch, 1977. ISSN 04-239-77
[2] Drkal, F.; Technika prostředí, 1978. ISSN 57-634-78
[3] Chyský, J., Hemzal,K. a kol.: Technický průvodce "Větrání a klimatizace". Bolit, 1993
[4] ASHRAE Handbook 2001 Fundamentals, 2001, ASHRAE, Atlanta. ISBN-1-883413-87-7
